Disclaimer: I have taken the help of ChatGPT to describe some of the more technical concepts in this write up, like definitions and explanations. Everything else, are my words.
In this series of posts I will try to build out a toolbox for data analysts. A basic understanding of statistics is critical for any data analyst or data scientist. While statistics as a subject is vast and capable of inducing cold sweats in most people due to its seemingly complex nature, it is also misunderstood and perhaps the most used concepts are simple enough for a person with basic math skills.
For example, today’s topic of basic descriptive statistics. Mean, median, mode, range, variance and standard deviation. For a given dataset, and for a single value:
Mean: The average of a dataset.
Median: The middle value of a dataset.
Mode: The most frequent value in a dataset.
Range: The difference between the highest and lowest values.
Variance: A measure of how spread out the values are.
Standard Deviation: The square root of the variance.
These terms are pretty self explanatory. But Variance and Standard Deviation may need more explanation. Here are the definitions in a bit more detail.
Variance
Definition: Variance is a measure of how spread out the values in a dataset are around the mean. It quantifies the extent to which each number in the dataset differs from the mean.
Standard Deviation
Definition: Standard deviation is the square root of the variance. It provides a measure of the average distance of each data point from the mean and is expressed in the same units as the data.
How to calculate?
These metrics are extremely easy to calculate with a simple python code. In my example here, I am using the House Prices dataset downloaded from Kaggle. The column in the dataset we are analyzing is: SalePrice which is the price of the house. The python code, which can very easily be generated by ChatGPT. Here is an example:
[python]
import pandas as pd
# Load the dataset
data = pd.read_csv('train.csv')
# Calculate descriptive statistics
mean_price = data['SalePrice'].mean()
median_price = data['SalePrice'].median()
mode_price = data['SalePrice'].mode()[0]
range_price = data['SalePrice'].max() - data['SalePrice'].min()
variance_price = data['SalePrice'].var()
std_dev_price = data['SalePrice'].std()
# Print the results
print(f"Mean: {mean_price}")
print(f"Median: {median_price}")
print(f"Mode: {mode_price}")
print(f"Range: {range_price}")
print(f"Variance: {variance_price}")
print(f"Standard Deviation: {std_dev_price}")Use Case and Pitfalls
Descriptive statistics may not be as “fancy” or “complex” as other statistical methods but they are crucial. For example, the mean value of a dataset can give us a fair idea of what the data looks like. Specially useful in pricing and sales. For example, in my job, I use these measures for understanding the price of our product offering as compared to other similar products. Median and Mode are also helpful in understanding where our product price lies if I were to lay down all similar products in the market on a table in front of me. Are we close to middle or are we too pricey.
One thing to take note is the word “similar”. When I say “similar” products, its important to understand what that means. Lets say we are trying to understand better if an online course I am selling is priced correctly or not. If I compare all available courses online (irrespective of what the course topic is) then my descriptive statistics will be misleading. Not all courses are created equal. Not all courses deliver the same value. And I cannot really compare a course which teaches you a technical skill and a course which is soft skills focused. The average price for my technical course may be too low (or too high).
While an AI tool can help you write the code, its in the data gathering phase where a human intellect is required. For these descriptive statistics to make sense, we must compare similar courses. And the “similarity” can be a complex. How deep should I categorize the data collection ? Should I look at all course prices of the same subject? Or should I look at all course prices of the same topic?
Inversely, if you already have a dataset, then these statistics can be used to understand the quality of the data. For example, continuing with our online course prices example, if the median and mean have a massive difference, then we are probably looking courses which are vastly different. If the variance or standard deviation of the course prices is too high, we are either looking at very different courses or we have an error in our data or we have an “outlier”. So these descriptive statistics can be used as a data quality measurement tool as well.
Results

From a house prices perspective, these results look accurate. The mean and median are not “wildly different” suggesting a uniform dataset, perhaps house prices from a zipcodes not too far from each other.
The high value of the range suggests that cheapest and the most expensive house have a massive difference, which can be true. But this is something to investigate.
The standard deviation is also high suggesting that there is either a big difference between the house prices or there are certainly some outliers. Further investigation is required.
Whats next?
I would probably do a histogram of the prices to understand how the dataset looks like. I already did and here are the results.
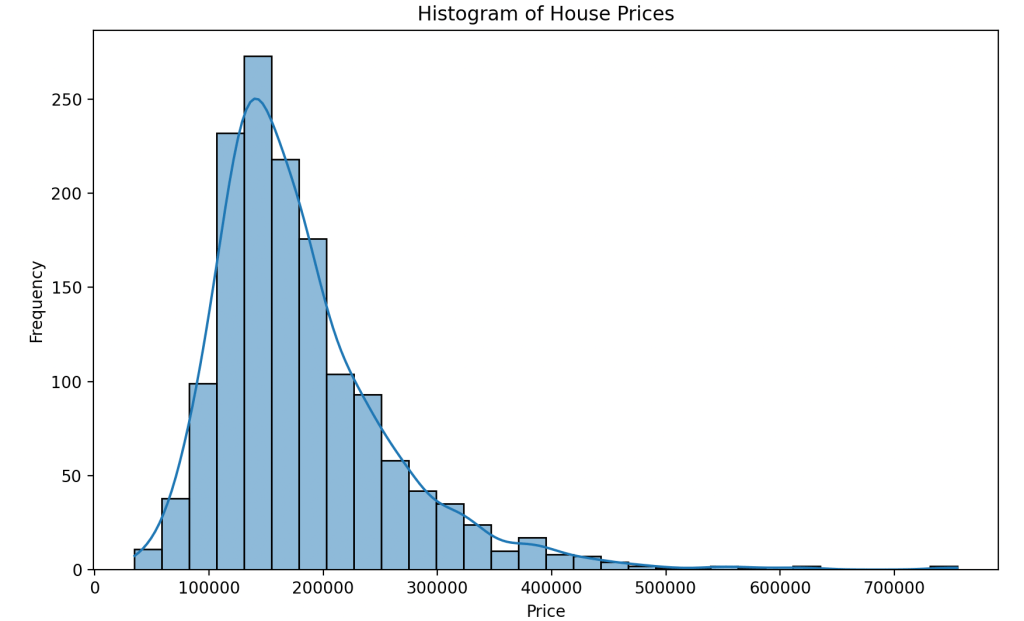
Looks like we have a significant number of houses which are above 200K . There is greater variability in prices above 200K suggesting that could be the reason for the high standard deviation.
Hopefully this was brief enough and useful enough! See you in the next one.
More Use Cases (Thanks ChatGPT!)
Finance:
- Variance: In finance, variance is used to measure the volatility of a stock’s returns. A higher variance indicates a more volatile stock.
- Standard Deviation: Standard deviation is used to gauge the risk associated with an investment. A higher standard deviation means more risk as the investment returns are more spread out from the mean.
Quality Control:
- Variance and Standard Deviation: In manufacturing, these measures help ensure product consistency. Low variance and standard deviation indicate that the product quality is consistent, with minimal deviation from the desired specifications.
Healthcare:
- Variance and Standard Deviation: In medical research, these measures help analyze the effectiveness of treatments. They can indicate how varied patients’ responses are to a treatment.